| Fenster schliessen | veröffentlicht | 04.09.2015 |
| Copyright | Dr.- Ing. Albert Ott Wiesbaden | |
| Prof. Dr.- Ing. Albert Ott, Wiesbaden | ||
| 2D Fourier Rückfaltung - der Weg zu virtuell punktförmig messenden elektromagnetischen Sonden | ||
|
Meßsonden in der zerstörungsfreien Werkstoffprüfung sind Sensoren, welche eine Werkstoff-Kenngröße in ein elektrisches Signal umwandeln und damit der elektronischen Signalverarbeitung zugänglich machen. Meist handelt es sich um Sonden, die mit elektromagnetischen Feldern arbeiten, beispielsweise magnetische, magnetinduktive oder Wirbelstrom- Sonden. Dabei wird durch eine elektronische Baugruppe in der Sonde, die an den Werkstoff herangebracht wird, ein elektromagnetisches Feld angeregt; dieses dringt in den Werkstoff ein, erzeugt dort Sekundärströme, die auf die Sonde zurückwirken, was sich in einem meßbaren Signal am Ausgang der Elektronik-Baugruppe zeigt. Für andere physikalische Meßprizipien gilt das Gesagte sinngemäß in gleicher Weise. |
||
|
|
||
|
Praktisch realisierte Meßsonden mit endlicher Baugräße treten stets mit einem endlich ausgedehnten Bereich des WerkstoffesMeßsonden in Wechselwirkung, so daß sich im Sondensignal nicht die Kenngröße eines Werkstoffpunktes abbildet, wie man es meist gerne hätte. Vielmehr trägt ein Werkstoffbereich zum Signal bei, was vor allem dann stört, wenn man beispielsweise bildgebende Verfahren zur Darstellung der Kenngröße einsetzen will. Durch geeignete mathematische Algorithmen läßt sich jedoch in Verbindung mit einem Scanning-Verfahren eine quasi punktförmige Darstellung aus dem zunächst gemittelten Signal zurücckgewinnen. Das Verfahren hierzu wird im folgenden beschrieben. |
||
|
|
||
|
In Bild 2 ist w(x) eine zu messende Werkstoffkenngröße. Die Meßsonde wird an der Stelle x an den Werkstoff herangebracht, bei berührenden Messungen wird sie dort aufgesetzt. Die Sonde arbeitet zusammen mit der Sondenelektronik im nachrichtentechnischen Sinn als Übertragungssystem, welches durch Multiplikation der Werstoffkenngröße w mit dem Sondenübertragungsfaktor s das Abtastsignal a liefert. |
||
|
|
||
Wäre die Sonde sehr klein, im Grenzfall punktförmig, so hätte man im Idealfall die Kenngröße w genau an der Stelle x gemessen. Nahezu jede praktisch ausgeführte Meßsonde hat jedoch wegen ihrer endlichen Baugröße einen gewissen Empfindlichkeitsbereich innerhalb dessen die Kenngröße w nach Maßgabe der lokalen Sondenempfindlichkeit zum Ausgangssignal a beiträgt. Man erhält somit einen gewichteten Mittelwert von w gemäß der Gleichung |
||
|
|
||
|
Die Integralgrenzen sind die linke und rechte Grenze an denen der Übertragungsfaktor der Sonde die Werte 0 erreicht hat. Geht man von der meist erfüllten Voraussetzung aus, daß die Sonde jenseits dieser Grenzen keine Werkstoffdaten mehr erfassen kan, dann kan man die Grenzen auf +/ - Unendlich ausdehnen; diese Annahme ist für die folgenden Berechnungen eine wichtige Voraussetzung und führt auf die Gleichung (3).. |
||
|
|
||
|
Die Idealform einer "punktgenauen" Messung von w(x), wie sie in Gleichung (1) zum Ausdruck kommt,. ist damit zuächst leider nicht möglich. Durch Anwenden eines geeignete Algorithmus läßt sich unter bestimmten Voraussetzungen die in (3) ausgedrückte Mittelung jedoch wieder rückgängig machen und dadurch eine örtlich hochauflösende Messung der Werkstoffkennkröße w(x) erzielen. Dies leistet die Fourier-Transformation und die damit zusammenhängende Operation der Faltung bzw. Rückfaltung des zunächst gewonnenen Signales a(x). Dazu wird (3) durch eine Koordinatentransformation (4) in die Form (5) umgewandelt. (hier evtl. Hinweis auf Korrelation) |
||
|
|
||
|
Gleichung (5) enthält nicht mehr die Variable xs des Koordinatensystems der Sonde, sondern nur noch die übergeordneten Koordinate x für die Sondenposition und x als laufende Koordinatenvariable. Die Übertragungsfunktion s der Sonde werde nun als symmetrisch zur Sondenmittelachse bei xs = 0 angenommen (6), woraus Gleichung (7) entsteht. |
||
|
Gleichung (7) hat genau die Form, die in der Theorie der Fourier - Transformation als Faltungsintegral bekannt ist. Dies eröffnet den Weg für eine weitere Bearbeitung mit dem Ziel, die gewünschte Funktion w(x) in hochaufgelöster Form zurückzuerhalten. Dazu wird im ersten Schritt Gleichung (7) fouriertransformiert (vergl. Anhang Gleichung ().was auf (8)und ausführlich geschrieben auf (9) führt. Durch eine Substitution (10) läßt sich die e-Funktion aufspaltem, die Bestandteile werden den Funktionen w und s zugeordnet. Durch Vertauschen der Reihenfolge der Integrationen ensteht Gleichung (11), in der sofort zu erkennen ist, daß sie aus dem Produkt der beiden Fouriertransformierten W(f) aus w(ξ) und S(f) aus s(xs) besteht, Gleichung (12). |
||
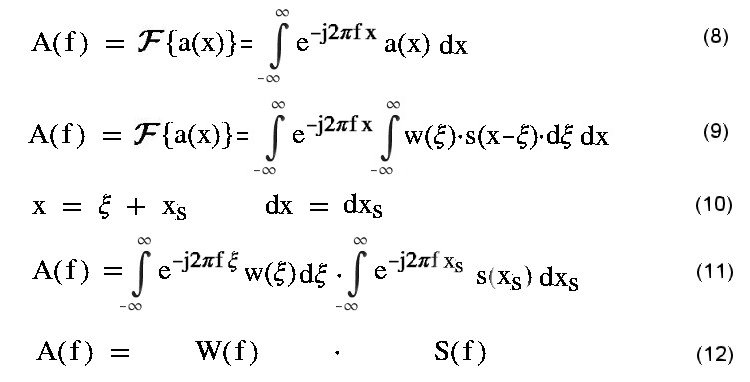 |
||
|
Die Funktion W(f) läßt sich damit als Quotient
von A(f) und S(f) darstellen und einer Fourier-Rücktransformation
unterziehen, was unmittelbar auf die Funktion w(x) der
Werkstoffkenngröße führt gemäß Gleichung (13). Der beschriebene Weg ist
die Operation der Rückfaltung des Faltungsintegrals Gleichung (7).. |
||
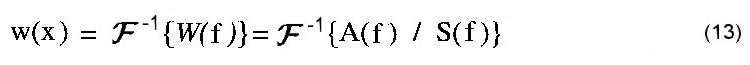 |
||
|
Die bisherigen Überlegungen bezogen sich eindimensional auf eine Abhängigkeit der Werkstoffkengröße w und des Sondenübertragungsfaktors s nur von der Koordinate x. In manchen Anwendungen mag eine solche Darstellung einer Abtastzeile bereits genügen; jedoch bereits bei bildhafter Darstellung der Kenngröße w ist eine Erweiterung in die zweite Dimension erforderlich. Die eindimensionale Gleichung (7) führt dann zur zweidimensionalen Gleichung (14). |
||
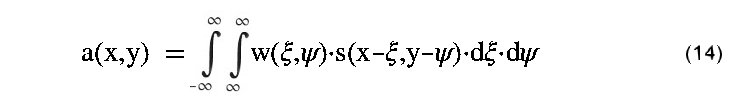 |
||
| In dem nun zu
bildenden Doppelintegral sind die Grenzen rechnerisch minus/plus
Unendlich; die endliche Ausdehnung des Sondenfeldes in beiden
Dimensionen sorgt jedoch dafür, daß die Integrale endlich bleiben, da
außerhalb der Empfindlichkeitsgrenzen der Sondenübertragungsfaktor s zu
Null wird.. So wie oben Gleichung (7) in Gleichung (8) eindimensional fouriertransformiert wurde, wird a(x,y) nach (14) in (15) zweidimensional transformiert. Die zweimiensionale Transformation kann dabei in zwei aufeinanderfolgende eindimensionale Transformationen zerlegt werden, wie dies der Vergleich der Gleichungen (15) und (16) zeigt, wobei die Reihenfolge der Transformationen hinsichtlich der beiden Koordinatenrichtungen natürlich gleichwertig ist. Im gezeigten Beispiel wird zuerst in x-Richtung transformiert bei zuächst konstant gehaltenem y. |
||
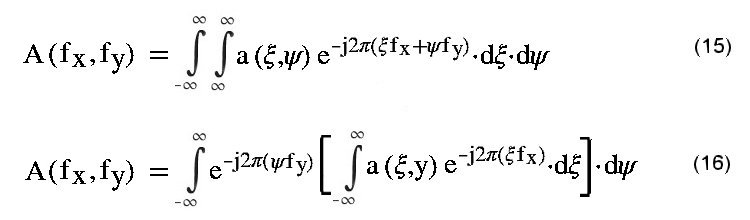 |
||
|
Ähnliche Transformationen wie in (15) für A(x,y) gezeigt gelten solche für W(x,y) in (17) und S(x,y) in (18). Diese Zusammenhänge und die zugehörigen Rücktransformationen werden benötigt, wenn im zweidimensionalen Fall nun die Bestimmung der gesuchten zweidimenionalen Werkstoff-Funktion w(x,y) erfolgen soll. |
||
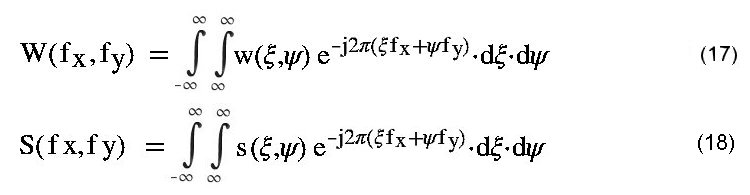 |
||
| Analog zum eindimensionalen Fall der Gleichungen (12) und (13) gelten im zweidimensionalen die Gleichung (19) und (20). | ||
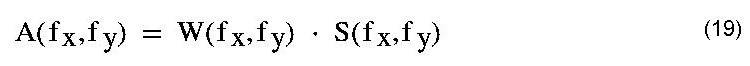 |
||
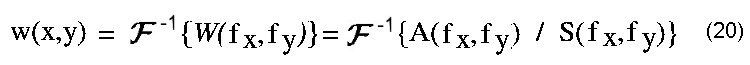 |
||
|
Bei der Anwendung der Gleichungen (13) und (20) für die Schlußauswertung werden die Sondenfunktionen S(f) bzw. S(fx,fy) benötigt. Diese Funktionen sind entweder aus den Konstruktionsdaten der Sonde bekannt oder berechenbar, sie können jedoch auch experimentell für eine Sonde bestimmt werden. Dazu wird eine abgewandelte Form der Gleichungen (13) oder (20) verwendet wie in (21) und (22) gezeigt. |
||
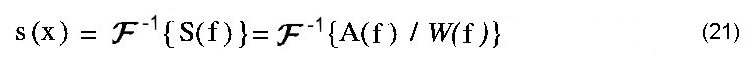 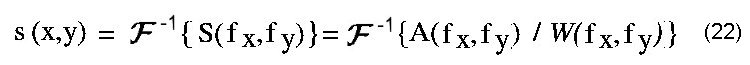 |
||
|
Hier werden die gesuchten Sondenfunktionen aus bekannten Werkstoff-Funktionen bestimmt. Man kann diesen Vorhang auch als Kalibrierung der Sonde hinsichtlich ihrer Ortsauflösung bezeichnen. Die Werkstoff-Funktion stellt man in Form eines Kalibrier-Normales zur Verfügung, also eines Werkstoffes mit bekanntem Verlauf der Größe w(x,y). Dies kann beispielsweise durch einen metallografisch bestimmten Funktionsverlauf der Kenngröße an einem Normal erfolgen, welches man anschließend in einem Kalibriervorgang mit der Sonde abtastet und das Abtastsignal mit Gleichung (21) oder (22) auswertet. Wegen der Vielzahl der Sondenprinzipien und -bauformen kann an dieser Stelle nur eine derart allgemein gehaltene Angabe gemacht werden. |
||
| In Kürze wird hier als Beispiel das Ergebnis einer Berechnung gezeigt, bei der anhand zweier Bilder die Erhöhung der Sondenauflösung durch das beschriebene Verfahren dargestellt wird. | ||
| Fenster schliessen | ||